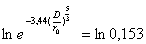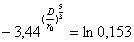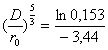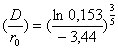www.epsilon-lyrae.de
zur Startseite zurück
 eine Ebene zurück
Kontakt
Datenschutzerklärung

Inhalt :

 Wie gut muss das Seeing sein ?

Stichworte : Auflösungsvermögen, Rayleigh-Kriterium, Seeing, Modulations Transfer Funktion (MTF), Kohärenzlänge, lucky short-exposure image

von J. S. Schlimmer (aus NightSky 3/2004)

Einleitung

Wie gut muss das Seeing sein damit man einen Doppelstern von 1,0 Bogensekunden noch auflösen kann ? Diese Frage stellte sich mir vor einigen Jahren als ich anfing Doppelsterne zu beobachten. 
Da sich diese Frage zunächst nicht beantworten ließ, wandelte ich sie dahingehend ab, in dem ich mir überlegte, wie kurz die Belichtungszeiten einer Webcam sein müssen, damit das Seeing eingefroren wird [1]. Natürlich lassen sich mit einer Webcam entsprechend kurze Belichtungszeiten realisieren, jedoch wird die Bildausbeute immer geringer, je schlechter das Seeing ist. Der Grund liegt in der Zerstörung der Wellenfronten durch die Luftunruhe. Somit blieb die ursprüngliche Frage nach dem Seeing zunächst unbeantwortet.
Kürzlich beschäftigte ich mich mit der Modulations Transfer Funktion (MTF) der Luft [2] und erkannte im Nachhinein, dass die Antwort für Langzeitbelichtungen tatsächlich ganz einfach ist und sie sich sogar präzise mathematisch berechnen läßt ! Man muss nur den Kontrast, der sich aus dem Rayleigh-Kriterium ergibt mit der MTF der Luft gleich setzen. Doch dazu gleich mehr.
Der zweite Teil dieses Beitrags beschäftigt sich mit der Frage, mit welcher Häufigkeit eine Webcam ein gutes Bild in Abhängigkeit vom Seeing aufzeichnet – oder anders ausgedrückt: lässt sich die Ausbeute guter kurzzeitbelichteter Einzelbilder eines Videos in Abhängigkeit vom Seeing abschätzen ?
 

Das Auflösungsvermögen und das Rayleigh-Kriterium

Durch die endliche Öffnung des Teleskops und den Wellencharakter des Lichtes wird ein idealer Punkt im Unendlichen (Stern ohne Luftunruhe) als Beugungsscheibchen endlicher Größe (Airy - Disk) in der Fokalebene abgebildet. Damit hängt das theoretische Auflösungsvermögen also von der Größe der Teleskopöffnung (Eintrittspupille) und der Wellenlänge des Lichtes ab. Die Auflösung lässt sich wie folgt berechnen :

Gleichung 1
Dabei ist D die effektive Öffnung des Teleskops. Möchte man das Ergebnis in Bogensekunden erhalten, so muss man Gleichung 1 mit 360°/2Pi x 3600 multiplizieren. Doppelsterne sind im Vergleich zu HII Regionen oder Galaxien helle Objekte, die im Okular direkt sichtbar sind. In der Regel können die Farben der einzelnen Komponenten deutlich wahrgenommen werden. Die maximale spektrale Empfindlichkeit des Auges für Farbwahrnehmungen (Zäpfchen) liegt bei 555 nm (DIN 5031 T 3) [7].
Zur Definition des Auflösungsvermögens eines Teleskops verwendet man sehr gerne das so genannte Rayleigh-Kriterium. Bei dem Rayleigh-Kriterium geht man davon aus, dass sich zwei Beugungsscheibchen gleicher Helligkeit und Farbe noch trennen lassen, wenn das Minimum des ersten mit dem Maximum des zweiten zusammenfällt. 



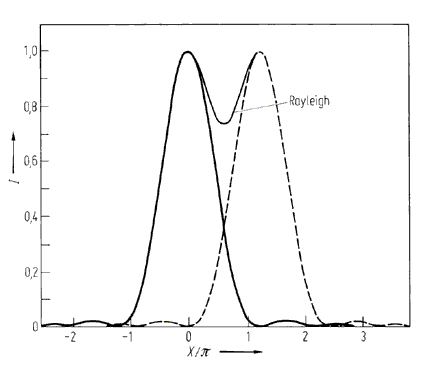
Abbildung 1 : Nach dem Rayleigh-Kriterium überlagern sich die Beugungsscheibchen eines Doppelsterns gerade so, dass das Minimum des ersten mit dem Maximum des zweiten zusammenfällt. Abbildung aus [3]

Ein Teleskop mit 8-Zoll Öffnung hat eine theoretische Auflösung von 0,70 Bogensekunden. Zwischen den beiden sich überlappenden Beugungsscheibchen fällt die Helligkeit auf 0,735 des Maximalwertes ab. Da es sich bei der Überlagerung der beiden Beugungsscheibchen um inkohärentes Licht handelt (jeder Stern stellt eine unabhängige Lichtquelle dar), entsteht kein Interferenzmuster im Überlappungsbereich. Damit lässt sich der Kontrast für einen gerade noch aufzulösenden Doppelstern wie folgt leicht berechnen :

Gleichung 2
Aus dem Rayleigh–Kriterium folgt also ein Kontrast von 15,3 % !
 

Die Modulations Transfer Funktion (MTF)

Die Modulations Transfer Funktion (MTF) beschreibt allgemein den Kontrast einer Bildübertragung in Abhängigkeit von der Auflösung (Schärfe). Jedes optische System (Teleskop, Okular, CCD, Film) hat seine eigene MTF. Auch die Bildübertragung durch die Luft lässt sich durch eine zeitlich gemittelte MTF ausdrücken [4] :

Gleichung 3
Der Parameter D beschreibt die Teleskopöffnung, r0 ist der Fried Parameter bzw. die Kohärenzlänge, mit der sich das Seeing beschreiben lässt. Eine ausführliche Darstellung hierzu findet der interessierte Leser unter [2].



Abbildung 2 : Die MTF der Luft für eine Kohärenzlänge r0  von 0,18 m
 

Zusammenhang zwischen dem Seeing und der Kohärenzlänge

Der Zusammenhang zwischen Seeing und Wellenlänge ist gegeben durch :

Gleichung 4
Um das Ergebnis in Bogensekunden zu erhalten muss man die Wellenlänge mit 360°/2Pi x 3600 multiplizieren.

Wie gut muss das Seeing sein für...... (Langzeitbelichtung)

Damit ein Doppelstern nach dem Rayleigh–Kriterium noch getrennt werden kann muss die  MTF(r0) = 0,153 sein. Nun können wir also mit der Rechnung beginnen. Hierzu müssen wir Gleichung 3 nach r0 auflösen. Den Exponent zur Basis e beseitigen wir zunächst durch den natürlichen Logarithmus




 

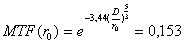
Als nächstes beseitigen wir den Exponenten in dem wir die 5/3-te Wurzel ziehen. Diese ist gleich dem Kehrwert des Exponenten. 

Zuletzt lösen wir die Gleichung nach r0 auf :
Gleichung 5
Um einen Doppelstern von 1,0 Bogensekunden aufzulösen, wird eine Öffnung D von 0,126 m benötigt (Gleichung 1).

Nun können wir die erste Frage beantworten : Die Kohärenzlänge (Fried Parameter) r0  beträgt 0,18 m (Gleichung 5). Dies entspricht bei einer Wellenlänge von 500 nm einem Seeing von  omega = 0,57 Bogensekunden (Gleichung 4). In Abbildung 2 ist die MTF bereits für diesen Wert dargestellt. Wie schon in [2] diskutiert, gilt die oben dargestellte MTF nur für fotografische Aufnahmen.

Die Wahrscheinlichkeit für ein gutes Einzelbild mit einer Webcam (Kurzzeitbelichtung)

Mit dem Aufkommen der CCD Kameras in den 70er Jahren und der damit verbundenen Möglichkeit mit kurzen Belichtungszeiten die Luftunruhe einzufrieren, stellte sich die Frage, wie viele Bilder aufgenommen werden müssen, damit man bei einem bestimmten Seeing ein gutes Bild erhält. Die besten Bilder werden dann zentriert und miteinander überlagert (Shift and add Verfahren, heute allgemein als Stacking bezeichnet). Durch die zunehmende Verbreitung moderner, lichtempfindlicher Videokameras wurde diese Technik Ende der 90er Jahre von einigen Amateurastronomen aufgenommen. Seit der Einführung preiswerter, lichtempfindlicher Webcams hat sich diese Technik in der Amateurastronomie als eigener Bereich etabliert.
Auch bei der Überlegung nach der Häufigkeit eines guten Bildes mit kurzen Belichtungszeiten war es der Physiker D. L. Fried, der als erster eine quantitative Lösung für diese Fragestellung fand [5]. Er nannte diese Bilder ”lucky short-exposure images”. Durch die Luftturbulenzen werden die ebenen Wellenfronten zerstört. Für ein gutes Bild (lucky image) sollen die Fehler über der gesamten Öffnung kleiner gleich 1 rad sein, also


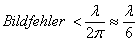
Abbildung 3 zeigt ein simuliertes Beugungsscheibchen für einen f/4 Newton mit 30 % Obstruktion zunächst ohne Seeing Effekt und dann mit einer Turbulenz von lambda / 2Pi , also ein ”lucky image”. 


Abbildung 3 : a) simuliertes Beugungsscheibchen für einen f/4 Newton mit 30 % Obstruktion b) simuliertes Beugungsscheibchen für einen f/4 Newton mit 30 % Obstruktion und einem Wellenfrontenfehler von 1 rad [6]

Natürlich zeigt sich der Seeing Effekt in der Natur nicht so symmetrisch wie in obiger Simulation. Doch kommen wir nun zurück zur Frage wie viele Bilder wir mit einer Webcam aufzeichnen müssen, um ein gutes Einzelbild zu erhalten. Die Wahrscheinlichkeit hierfür ist annähernd [5] :

  Gleichung 6
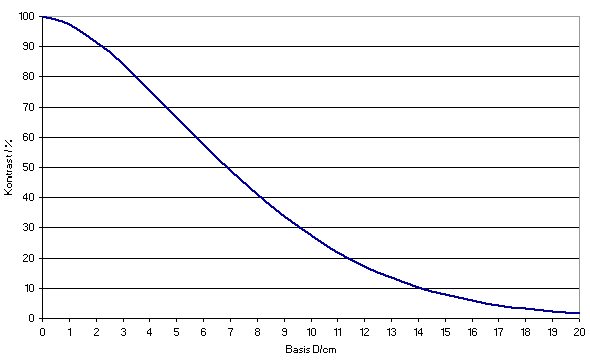
In Gleichung 6 beschreibt D wieder die Teleskopöffnung und r0 die Kohärenzlänge. Dabei muss D/r0  größer gleich 3,5 sein. In Abbildung 4 ist die Wahrscheinlichkeit für 8 Zoll-, 12 Zoll- und 16 Zoll Öffnungen berechnet. 


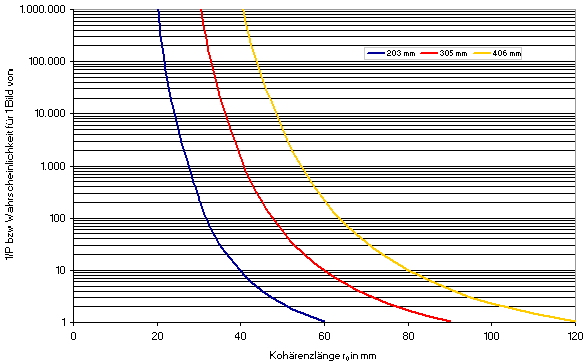
Abbildung 4 : Die Wahrscheinlichkeit P für ein ”lucky image” für 8-, 12- und 16 Zoll Öffnungen in Abhängigkeit der Kohärenzlänge r0

Wie man sofort erkennt, liefert ein 8 Zoll Teleskop bei einer Kohärenzlänge von 60 mm (Seeing ca. 1,7 Bogensekunden) jedes Bild besser als lambda / 2Pi, während ein Teleskop mit 16 Zoll Öffnung zur Erfüllung dieser Bedingung bereits 223 Bilder benötigt ! Ist also nun ein Teleskop mit kleiner Öffnung im Vorteil ? Nein, natürlich nicht, denn jedes Bild eines 16-Zöllers, das die Bedingung erfüllt, hat dafür ja schließlich auch die doppelte Auflösung. 
Bei genauer Betrachtung der Gleichung 6 fällt auf, dass in der Berechnung der Wahrscheinlichkeit P die Belichtungszeit nicht enthalten ist. Das ist auch nicht notwendig, denn die Belichtungszeit ist in der Bedingung für ein gutes Bild bereits indirekt enthalten. Sie muss so kurz sein, dass das Seeing eingefroren wird.

Zusammenfassung

Es ist möglich für die Langzeitbelichtung (z. B. Galaxien, Nebel u. ä.) das reale Auflösungsvermögen von Objektdetails in Abhängigkeit der Luftunruhe zu berechnen.
Weitaus interessanter ist es jedoch, in der Videoastronomie die Bildausbeute in Abhängigkeit von der Luftunruhe abschätzen zu können. Bei einem 8 Zoll Teleskop kann man bereits bei einem Seeing von 1,7 Bogensekunden davon ausgehen, dass der Wellenfrontenfehler kleiner als lambda / 2Pi ist.

Literartur, Quellennachweis

[1] J.S. Schlimmer, Gamma Virginis – oder der Sieg über das Seeing mit einem 8 Zoll Newton Teleskop, interstellarum 27, April 2003
[2] J.S. Schlimmer, Auflösungsvermögen und Modulations Transfer Funktion (MTF) in der Praxis, NightSky 2/2004, http://www.nightsky-online.de/
[3] G. D. Roth, Herausgeber, Handbuch der Sternfreunde in zwei Bänden, Band 1, Nachdruck der 4. überarbeiteten und erweiterten Auflage 1998, Springer Verlag
[4] Paul Titze, A Seeing Analyses for SUSI, http://www.physics.usyd.edu.au/~ptitze/work/seeing.htm
[5] D. L. Fried, Probability of getting a lucky short-exposure image through turbulence, Optical Society of America, Journal, vol. 68, Dec. 1978
[6] Die Abbildung wurde erstellt mit dem Programm Aberrator V3.0, http://aberrator.astronomy.net/index.html
[7] Naumann/Schröder, Bauelemente der Optik, Taschenbuch der technischen Optik, 6. Auflage, Carl Hanser Verlag 1992

 Seitenaufrufe seit 1. Januar 2005 :