www.epsilon-lyrae.de
zur Startseite zurück
eine Ebene zurück
Kontakt
Datenschutzerklärung


Inhalt :




Wilhelm Herschel
(1738-1822)



Friedrich Georg Wilhelm
Struve (1793-1864)



Johann Heinrich Mädler
(1794-1874)



Hippolyte Fizeau
(1819-1896)



K.A.Strand, US Naval Obs.
(1907-2000)



Wulff Heintz
(1930-2006)



Steffan Soderhjelm
Lund Observatory


 Gamma Virginis (ADS 8630) - Interferometrische Beobachtungen
der Periastronpassage

Interferometric measurements of the orbit of gamma Virginis = ADS 8630 = STF1670 within the range of the Periastron.

J.S. Schlimmer

1. Einleitung

Gamma Virginis ist ein bekanntes Mehrfachsystem im Sternbild Jungfrau. Seine beiden nahezu gleich hellen und gleich farbigen Komponenten A und B umlaufen dabei den Schwerpunkt in rund 169,1 Jahren. Die Bahn von Gamma Virginis ist stark elliptisch, so daß es während eines Umlaufs zu einer Annäherung der beiden Komponenten kommt. Zwischen 2002 und 2008 betrug der Abstand weniger als eine Bogensekunde. Die größte Annäherung fand im Frühjahr 2005 statt. Der Abstand betrug etwa 0,37". Ein aussichtsreiches Meßverfahren, diesen Bahnabschnitt indirekt zu beobachten, stellte die Interferometrie dar. Seit 2004 verfolgte ich die Periastronpassage auf diese Weise.

2. Rückblick

Bereits 1720 bestimmte der französische Astronom Cassini das erste Mal den Abstand und den Positionswinkel von Gamma Virginis. Er ermittelte 7,49“ für die Distanz und 139,7° für den Winkel. Aufgrund zahlreicher Beobachtungen bemerkten die Astronomen des 18. und 19. Jahrhunderts sehr schnell, daß sich beide Komponenten immer mehr annähern. J. Herschel versuchte als erster die Bahn durch eine Ellipse anzunähern, wobei er für die Umlaufzeit zunächst 525 Jahre, später sogar 660 Jahre annahm. Nach J. Herschels Prognose hätte Gamma Virginis einen minimalen Abstand von 0,51“ gehabt, doch mußte er feststellen, daß der Abstand immer kleiner wurde. Selbst bei außergewöhnlich guten Beobachtungsbedingungen gelang es ihm mit 480-facher Vergrößerung nicht mehr, Gamma Virginis mit seinem 20-Fuß-Teleskop (0,47 m) zu trennen. Nur W. F. Struve konnte in den Jahren 1833 bis 1836 den Abstand nahe des Periastrons bestimmen. Er ermittelte 1836 bei einem Positionswinkel von 151,34° einen Abstand von lediglich 0,257".

In den darauf folgenden Jahren wurden von verschiedenen Astronomen immer wieder Elemente zur Ephemeridenberechnung veröffentlicht. Die genaueste Berechnung vor der Perastronpassge 2005 stammt von S. Söderhjelm (1999). Er berücksichtigte auch die Daten der Hipparcos Satelliten Mission [5]. Obwohl die zuletzt vorgeschlagene Umlaufbahn erst wenige Jahre alt war, zeigten sich bereits ab dem Jahr 2002 erneut Abweichungen zwischen der vorhergesagten und der gemessenen Umlaufbahn. Dies machte den Periastrondurchgang von Gamma Virginis, der für das Frühjahr 2005 erwartet wurde, umso spannender. Aber auch in den kommenden Jahren bleibt die Verfolgung der Umlaufbahn spannend, denn es wird interessant sein festzustellen, ab wann Gamma Virginis wieder visuell getrennt werden kann. Nachfolgend sind einige Ephemeridenelemente gegenüber gestellt :

T
 a
 e
 i
 Omega
 omega
 Periode
Herschel 1830 [2]
 1834,010
 11,83
 0,8872
 68,0
 87,83
 290
 513,28
Mädler 1839 [1]
 1836,103
 -
 0,868
 35°58,04
 58°22,55
 265°59,95
 157,57
Doberck 1896 [16]
 1836,409
 3,721
 0,885
 106,39 33°21 27,9 184,47
Strand 1937 [15]
 1836,433 3,46
 0,881
 146,05
 31,78
 1900
 171,37
Heintz 1990 [3]
 2005,130
 3,697
 0,885
 148
 36,9
 256,5
 168,68
Söderjhelm 1999 [5]
 2005,100
 3,697
 0,885
 148
 37
 257
 168,90
Girard 2000 [10]
 1836,400
 3,680
 0,890
 148
 37
 257
 168,9
Scardia 2006 [12]
 2005,510
 3,643
 0,882
 149,4
 35,3
 255
 169,1
Docobo 2006 [12]
 2005,510
 3,644
 0,883
 149,1
 37,1
 256,7
 169,1
Mason 2006 [13]
 2005,438
 3,662
 0,8825
 148,82
 73,78 213,79
 168,93
Zirm 2007 [17]
 2005,530
 3,657
 0,8815
 149,0
 34,7
 254,5
 169,1
Tabelle 1 : Vergleich der Ephemeridenelemente

Darin sind :

1. T = Zeitpunkt des Periastrons (Punkt der kleinsten Distanz)
2. a = große Halbachse i.a. in AE
3. e = numerische Exzentrizität
4. i = Inklination (Bahnneigung zur Ekliptik)
5. Omega = Länge des aufsteigenden Knotens
6. omega = Argument des Periastrons
7. Periode = Umlaufdauer in Jahren
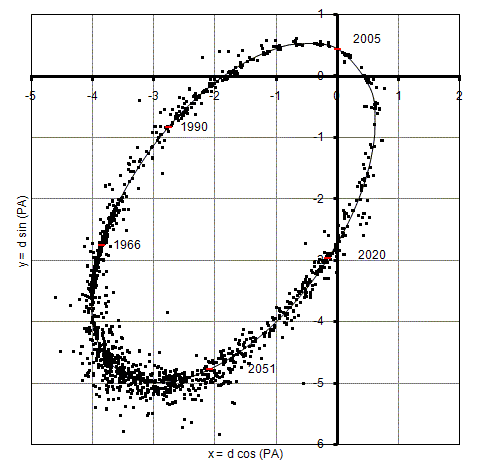
Gamma Virginis Orbit Sca2006b STF1670
Abbildung 2: Umlaufbahn nach Sca2006b sowie Messungen von 1777 bis 2008

Die verschiedenen Vorhersagen für den Zeitraum von 2005 bis 2010 finden Sie auf dieser Seite : Gamma Virginis : Ephemeriden für 2005 bis 2010.

 
3. Das interferometrische Meßprinzip

Das Meßprinzip ist recht einfach und funktioniert nach dem Prinzip der Beugung am Doppelspalt. Maskiert man die Teleskopöffnung mit einer Doppellochblende (sogenannte Subaperturen), so wird ein Stern durch jede der beiden Öffnungen separat abgebildet. Im Fokus überlagern sich die Lichtwellen beider Öffnungen und es entsteht ein typisches Muster aus hellen und dunklen Streifen. Dieses Muster wird allgemein als Interferenzmuster bezeichnet. Die Streifendichte hängt vom Abstand der beiden Öffnungen ab (Abbildung 3). 


Abbildung 3 : Interferenzstreifen bei der Abbildung eines Einzelsterns durch eine Doppellochblende bei a) kleiner Basis und b) bei größerer Basis mit einem rot-orange Filter.

Der Abstand der Öffnungen wird bei Interferometern als Basis B bezeichnet. Der Streifenabstand f läßt sich (in Bogensekunden) wie folgt berechnen :

Gleichung 1
Man bezeichnet diese Anordnung auch als Fizeau Interferometer. Fällt das Licht zweier eng benachbarter Sterne durch diese Öffnungen, so überlappen sich die Interferenzmuster der beiden Sterne im Beugungsscheibchen. Es läßt sich ein Positionswinkel PW und eine Basis B finden, bei der die hellen Streifen (Intensitätsmaxima) des einen Interferogramms auf die dunklen Streifen (Intensitätsminima) des anderen fallen. In diesem Fall ist der Streifenkontrast minimal und der Abstand s der beiden Komponenten läßt sich dann für das erste Minimum wie folgt berechnen :
Gleichung 2
Eine sehr einfache, aber ausführliche Darstellung über die Grundlagen eines Sterninterferometers finden Sie unter [6]. Um mit einer solchen Blende Messungen durchzuführen, muß die Basis variabel sein. Ferner muß die Blende drehbar angebracht werden, da die Achse der beiden Öffnungen gleich dem Positionswinkel sein muß. Zur Bestimmung der Separation von 0,35" ist bei einer Wellenlänge von 550 nm eine Basis von mindestens 16 cm für das 1. Kontrastminimum notwendig. Das zweite Kontrastminimum liegt bei einer Basis von 47,3 cm. Diese läßt sich aber mit einem 8-Zoll-Teleskop nicht mehr realisieren. Hierzu müßte man auf das Design von Michelson´s Sterninterferometer zurück greifen, mit dem er 1920 den scheinbaren Durchmesser des roten Überriesen Beteigeuze bestimmte. 

4. Die Kontrastfunktion

Für enge Doppelsterne ist der Kontrast der Interferenzstreifen bei korrektem Positionswinkel proportional dem Betrag der Kosinus-Funktion (Abbildung 4). Der Kontrast der Interferenzstreifen nimmt mit größer werdender Basis so lange ab, bis der gesuchte Abstand gefunden ist. Vergrößert man die Basis über diesen Abstand hinaus, so werden wieder Interferenzstreifen sichtbar. Man kann daher den gesuchten Abstand von zwei Seiten her bestimmen. Die gesuchte Basis korrespondiert mit dem Nulldurchgang der Kontrastfunktion.


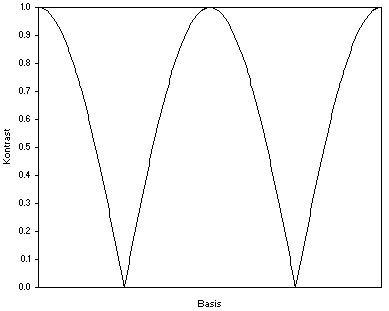
Abbildung 4 : Die Kontrastfunktion bei der interferometrischen Beobachtung enger Doppelsterne

Interessanterweise hat die Kontrastfunktion gerade am gesuchten Nullpunkt ihre größte Empfindlichkeit, da hier die Steigung der Kosinus-Funktion am größten ist (Maximum der 1. Ableitung). Da keine negativen Intensitätswerte möglich sind, erfährt das Interferenzmuster am Nullpunkt einen Phasensprung, was sich in Form einer Kontrastumkehrung sichtbar macht. Dies ist aber für unsere Betrachtungen ohne Belang.

Durch die Luftunruhe und andere limitierende Faktoren ist es in der Praxis jedoch nicht möglich, den Nullpunkt der Kontrastfunktion exakt zu bestimmen. Bereits kurz vor oder nach dem Nullpunkt können die Interferenzstreifen nicht mehr erkannt werden. Durch beidseitiges Messen lässt sich der Nullpunkt anschließend durch Bildung des Mittelwertes ermitteln.

In der Praxis hängt die Sichtbarkeit der Interferenzstreifen auch von der Helligkeit des Beugungsscheibschens und somit von der Form und Fläche der Öffnungen ab. Zu kleine Öffnungen lassen zu wenig Licht für eine deutliche Beobachtung der Interferenzstreifen durch, zu große Öffnungen schränken gerade bei kleineren Teleskopen die maximale Basis stark ein, ferner wächst der Seeingseinfluß mit zunehmender Öffnung. Nach meinen Erfahrungen läßt sich der Nulldurchgang bis auf 1 mm genau bestimmen.

 
5. Ein einfaches Sterninterferometer

Das Interferometer besteht aus einer 250 mm x 250 mm x 2 mm dicken Trägerplatte aus Polystyrol, die auf einem 30 mm tiefen und 230 mm breiten Zylinder befestigt ist. Der Zylinder sitzt auf dem frontseitigen Tubusende. An dem Zylinder ist eine Skala angebracht, womit Winkel bis 0,5° erfaßt werden. In die Trägerplatte wurde ein rechteckiges Loch geschnitten. An den Längsseiten befinden sich Führungen zur Aufnahme der Blenden. Auf den Führungen sind ebenfalls zwei feste Skalen angebracht, deren kleinste Unterteilung 1 mm ist. Diese ermöglichen ein bequemes Ablesen und Einstellen der Basis. Die Blenden sind so angefertigt, dass sie schnell gegeneinander ausgetauscht werden können.

 

Abbildung 5 : Ein einfaches Sterninterferometer mit 50 mm Lochblende (links) und Interferometeraufsatz mit Schlitzmaske (rechts)

Es stehen Blenden verschiedener Formen und Größen zur Verfügung. Mit spaltförmigen Öffnungen lassen sich sehr lichtstarke Blenden realisieren. Auf Grund der Sphärischen Aberration meines Teleskops und der auffälligen Beugungserscheinungen, die beim Vixen R200SS generell durch die 5 mm dicke Sekundärspiegelhalterung hervorgerufen werden, können jedoch keine spaltförmigen Blenden eingesetzt werden. Die besten Erfahrungen konnten mit kreisförmigen Öffnungen mit einem Durchmesser von 40 mm bzw. 50 mm gemacht werden. Insbesondere bei den 40 mm Öffnungen stehen die beiden Interferenzmuster nahezu flimmerfrei übereinander. Da neben dem Seeing auch die Helligkeit des Beugungsscheibchens einen großen Einfluss auf die Genauigkeit der Messung hat, werden meist 50 mm große Öffnungen verwendet. Als Material wurden 0,5 mm dicke Polystyrol Platten verwendet. Dünne Polystyrolplatten lassen sich einerseits leicht bearbeiten, andererseits sind sie unempfindlich gegen Feuchtigkeit (Taubeschlag). Die Innenseiten sind matt schwarz lackiert.

6. Die Handhabung

a) Bestimmung des Positionswinkels PW :

Als erstes muß die Ausrichtung der Winkelskala anhand der scheinbaren Bewegung von Gamma Virginis bei ausgeschalteter Nachführung überprüft werden. Befindet sich das Teleskop auf einer Deutschen Montierung, so sollte man diese Überprüfung sowohl für die westliche als auch für die östliche Lage des Teleskops (in Bezug auf die Montierung) durchführen. Solange das Design des Interferometers nicht verändert wird, genügt eine gelegentliche Kontrolle.

Zur Bestimmung des Positionswinkels wird zunächst die Basis auf den ungefähren Wert für die zu erwartende Separation eingestellt. Nun wird die Achse des Interferometers so lange gedreht, bis sich ein Kontrastminimum (Methode 1) im Streifenmuster einstellt. Zur Minimierung des systematischen Fehlers sollte die Rotation der Blenden sowohl im Uhrzeigersinn als auch gegen den Uhrzeigersinn erfolgen. Das Ergebnis wird durch die Berechnung des Mittelwerts bestimmt.

Eine weitere Möglichkeit zur Bestimmung des Positionswinkels besteht in der Ermittlung des Kontrastmaximums (Methode 2). Dieses stellt sich ein, wenn die Achse der beiden Öffnungen mit dem Positionswinkel des Doppelsterns einen rechten Winkel bildet. Zur besseren Beurteilung des Kontrastmaximums wird ein Grünfilter (Meade Serie 4000, Nr.58) in den Strahlengang eingesetzt. Die durchgelassene Lichtmenge beträgt 24 %. Dadurch sind nur noch im Bereich des Kontrastmaximums die Interferenzstreifen sichtbar. Diese Methode hat jedoch einen Nachteil : die Empfindlichkeit des Verfahrens ist gerade am gesuchten Maximum Null, da die Steigung der Funktion an dieser Stelle ebenfalls Null ist (Minimum der 1. Ableitung).

b) Bestimmung der Distanz (Separation) s

Ausgangspunkt ist der ermittelte Positionswinkel. Für diesen werden die Blenden mittig auf die minimale Basis eingestellt. Je kleiner die Basis ist, umso größer ist der Kontrast der Interferenzstreifen. Durch gleichmäßiges Verschieben der beiden Öffnungen wird die Basis solange vergrößert, bis der Kontrast der Interferenzstreifen möglichst gering ist. Da die beiden Komponenten A und B von Gamma Virginis nahezu gleich hell sind, kann für die Öffnungen eine Basis gefunden werden, bei dem keine Interferenzstreifen im Beugungsscheibchen mehr zu beobachten sind. Wird die Basis weiter vergrößert, so lassen sich erneut Interferenzstreifen erkennen. Mit größer werdender Basis wächst aber auch die Streifendichte. Gleichzeitig nimmt der Kontrast mit wachsender Streifendichte bei der Betrachtung durch das Okular aufgrund der optischen Modulations Übertragungs Funktion (MTF) ab. Somit wird das Auffinden des Minimums mit wachsender Basis immer schwerer. Das bedeutet, je enger der Abstand der Doppelsternkomponenten ist, umso stärker muss die Vergrößerung sein, mit der das Interferenzstreifenmuster betrachtet wird. Die Beobachtung erfolgt mit 250-facher Vergrößerung.
Für die Bestimmung des Positionswinkels und des Abstandes sollte man ca. 1,5 bis 3 Stunden Beobachtungszeit kalkulieren.

7. Ergebnisse

Eine erste Version des oben beschriebenen Interferometers kam im Mai 2004 zum Einsatz. Ende März 2005 (2005,249) konnte dann die Beobachtung der eigentlichen Periastronpassage beginnen. Der Winkel konnte zunächst nur grob abgeschätzt werden. Die Interferenzstreifen wiederum ließen sich einseitig bis zu einer Basis von 137,3 mm (< 0,41”) verfolgen.
Am 11. April (2005,278) erfolgte eine weitere Messreihe. Für die Winkelmessungen kam eine neue, vereinfachte Blende mit einer festen Basis von 137 mm zum Einsatz. Diese Blende ermöglichte es, in kürzerer Zeit Winkelmessungen durchzuführen. Die Messung der Distanz erfolgte anschließend mit einer 50 mm Lochblende mit variabler Basis.

Diese erste Version des Interferometers hatte aber einen Konstruktionsfehler. Die Trägerplatte hatte lediglich eine Dicke von 0,5 mm. Beim Befestigen der Trägerplatte an den Zylinder verzog sich die Platte leicht, so daß beide Öffnungen stets ein wenig zueinander geneigt waren. Dieser Mangel wirkte sich auf die Kohärenz der Lichtwellen und somit auf den Kontrast des Interferenzmusters aus. Eine beidseitige Bestimmung des Nullpunktes war mit diesem Interferometer nicht möglich.

Eine verbesserte Form dieses Interferometers mit stabiler Trägerplatte kam ab dem 19. Mai (2005,381) für die Distanzmessung zum Einsatz. Erstmals konnte der Nullpunkt der Kontrastfunktion vollständig mit einer Genauigkeit von 1-2 mm durchlaufen werden. Mit den 40 mm Lochblenden konnten nach dem Nulldurchgang die Interferenzstreifen wieder bis zu einer Basis von 150 mm beobachtet werden. Der Positionswinkel wurde weiterhin mit einer vereinfachten Blende fester Basis bestimmt. Weitere Messungen folgten.

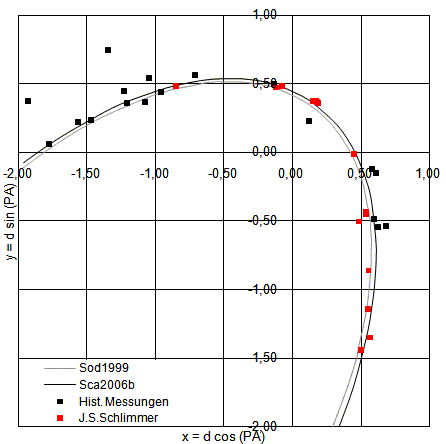
Abbildung 6 zeigt den von Söderhjelm (1999) und Scardia (2006) berechneten Bahnausschnitt für 1997 bis 2012. Die schwarz gekennzeichneten Punkte sind historische Meßergebnisse der Periastronpassage um das Jahr 1836. Es handelt sich dabei unter anderem um Messungen von Dawes, Struve, John Herschel, Smyth, Encke, Galle und Mädler [1]. Die rot dargestellten Punkte sind eigene Messungen der Periastronpassage von 2005.



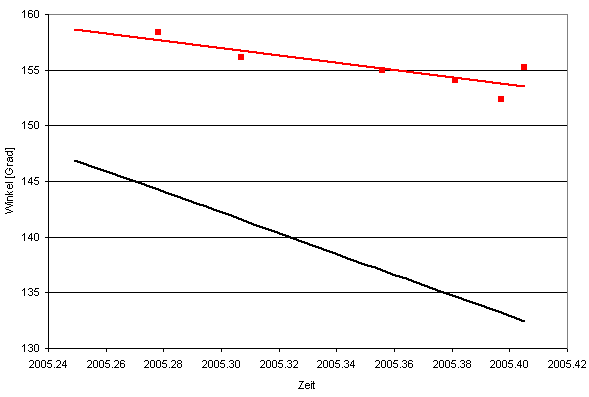
Abbildung 6 : Darstellung der berechneten Umlaufbahn für den Zeitraum von 1997 bis 2012 nach S. Söderhjelm und Scardia sowie historische Meßergebnisse dieses Bahnabschnittes von 1831 bis 1837 (schwarze Punkte). Die eigenen Messungen sind als rote Punkte gkennzeichnet.

In Abbildung 7 sind die Winkel über der Zeit aufgetragen. Die schwarze Kurve stellt die Winkel aus den Ephemeriden von Söderhjelm dar, die rote Kurve repräsentiert die experimentell ermittelten Winkel. Für kleine Zeiträume kann die Winkelgeschwindigkeit näherungsweise als konstant betrachtet werden. Aus dieser Darstellung wird die Abweichung zwischen vorhergesagter Winkeländerung und der ermittelten Änderung sehr deutlich.


Abbildung 7 : Positionswinkel im Bereich des Periastrons, Ephemeriden (schwarz) nach Söderhjelm, interferometrisch bestimmte Positionswinkel (rot)


8. Vergleich der interferometrischen Ergebnisse mit aktuellen Umlaufbahnen

Die Vergangenheit hat gezeigt, daß bislang alle vorgeschlagenen Ephemeriden nur bestimmte Bahnabschnitte hinreichend genau beschreiben konnten. Selbst neuere Berechnungen, die unter Zuhilfenahme von Satellitendaten durchgeführt wurden, konnten die Umlaufbahn von Gamma Virginis im Periastron nicht mehr exakt beschreiben. Bis 2001 stimmten die Meßwerte in [8] mit den nach Söderhjelm berechneten Werten überein, doch zeigten sich ab 2002 bereits erste Abweichungen des Positionswinkels von 0,7°. Diese Abweichungen vergrößerten sich bis 2004 auf rund 4°.

Inzwischen liegt der Periastrondurchgang einige Jahre zurück. Im Spätsommer 2006 wurden unabhängig voneinander 3 neue Bahnberechnungen veröffentlicht, die erstmals auch speckle-interferometrische Messungen der vergangenen Periastronpassage berücksichtigen (siehe Tabelle 2). Diese Umlaufbahnen tragen daher dem nachlaufenden Winkel von Gamma Virginis wesentlich besser Rechnung, wie die zuvor vorgeschlagenen Umlaufbahnen. Da alle neuen Bahnen im Prinzip auf den gleichen Meßdaten beruhen, ist es nicht weiter verwunderlich, daß sie fast identisch sind.

In Tabelle 8 sind die nach der Bahn von Scardia berechneten Werte [12, 14], meine eigenen Beobachtungen und die Residuen dargestellt. Die von mir interferometrisch ermittelten Werte stimmen gerade im Bereich des Periastrondurchgangs hervorragend mit den neu berechneten Ephemeriden überein.


 Eigene Messungen
 Ephemeriden nach Scardia Residuen
Datum
 s
 PW
 s
 PW
 s
 PW
2002,412*
 0,98''
 240°
 1,039" 243,0° -0,059" -3°
2004,430 0,49" 192° 0,575" 205,0° -0,085" -13°
2005,249 <0,41" 154° 0,399" 162,9° -
 -8,9°
2005,278 <0,41" 158° 0,395" 160,8° -
 -2,6°
2005,307 -
 155° 0,391" 158,6° -
 -3,6°
2005,356 -
 155° 0,386" 154,9° -
 0,1°
2005,381 0,417" 154° 0,383" 152,9° 0,034" 1,1°
2005,397 0,411" 152° 0,382" 151,7° 0,033" 0,3°
2005,405 0,414" 154° 0,381" 151,1° 0,033" 2,9°
2006,334 0,450" 88° 0,478" 84,3° -0,028" 3,7°
2007,277
 0,700''
 44°
 0,733''
 53,2°
 -0,033''
 -9,2°
2007,282
 0,692''
 51°
 0,734''
 53,1°
 -0,044''
 -2,1°
2007,290
 0,700''
 50°
 0,737''
 53,0°
 -0,037''
 -3,0°
2008,324*
 1,025''
 33°
 1,008''
 37,1°
 0,017''
 -4,1°
2009,299*
 1,270''
 26°
 1,239''
 28,2°
 0,031''
 -2,2°
2010,309*
 1,465''
 22,9°
 1,456''
 21,8°
 0,009''
 1,1°

Tabelle 8 : Vergleich zwischen beobachteten (J.S.Schlimmer) und kalkulierten Werten (Sca2006b), *in diesen Jahren wurden die Bahnwerte nicht mit Hilfe der Interferometrie sonder mit Hilfe einer Webcam bestimmt.

9. Fehleranalyse

a) Bestimmung der Distanz
 
Für eine beidseitige Bestimmung von Distanzen unter 0,4" reicht die maximale Basis, die mit 50 mm Subaperturen realisiert werden kann, nicht aus. Als Folge entsteht prinzipiell ein systematischer Fehler unbekannter Größe (siehe Kontrastfunktion). Der gefundene Distanzwert ist daher immer größer als der tatsächliche Abstand zwischen den beiden Komponenten von Gamma Virginis. Bei Distanzen größer 0,4" läßt sich der Nullpunkt der Kontrastfunktion zweiseitig bestimmen. Die Helligkeit der sich überlappenden Interferenzmuster reicht bei gutem Seeing aus, um noch 1 mm vor bzw. hinter dem gesuchten Nullpunkt Inhomogenitäten im Beugungsscheibchen zu erkennen (Messungen ab 2005,381). Bezogen auf die Kontrastfunktion (Abbildung 4) entspricht dies einem Winkel von 88,7° bzw. 91,3° ! Der Kontrast beträgt an dieser Stelle lediglich noch 2,3 %.

Die korrekte Messung der Distanz hängt auch vom Positionswinkel ab. Ein falsch eingestellter Positionswinkel wirkt sich mit dem Kosinus der Winkeldifferenz auf die gesuchte Basis aus. Für Winkeldifferenzen bis 15° ist der Fehler kleiner als 5 %.

Eine weitere Fehlerquelle ist die effektive Wellenlänge, die zur Berechnung der Distanz zugrunde gelegt wird. Beide Komponenten sind vom Spektraltyp F, die Oberflächentemperatur liegt zwischen 6000 K und 7500 K. Somit resultiert ein Strahlungsmaximum, das gegenüber der Sonne zu kleineren Wellenlängen hin verschoben ist. Für die Beobachtung der Interferenzstreifen ohne Filter sollte somit die effektive Wellenlänge kleiner gleich 550 nm sein.

b) Bestimmung des Positionswinkels

Zur Bestimmung des Positionswinkels ist die genaue Kenntnis der Distanz nicht notwendig aber sinnvoll. Auch mit einer zu kleinen bzw. zu großen Basis kann der Positionswinkel durch die Bestimmung des Kontrastminimums oder des Kontrastmaximums durch beidseitiges Messen (Rotation der Blende im Uhrzeigersinn und gegen den Uhrzeigersinn) gefunden werden. Allerdings ist dann mit einem größeren statistischen Fehler zu rechnen. Bei der Bestimmung des Kontrastmaximums liegt der gesuchte Positionswinkel senkrecht zur eingestellten Basis. Der Kontrast folgt bei der Bestimmung des Positionswinkels der Sinusfunktion. Die größere Empfindlichkeit ergibt sich somit für die Ermittlung des Kontrastminimums, da die Sinusfunktion für Winkel von 0° bzw. 180° die größte Steigung hat.

Ein großes Problem bei der Bestimmung des Kontrastminimums stellen die hellen Beugungserscheinungen dar. Diese werden durch die 5 mm dicken Sekundärspiegelhalterungen des Vixen R200SS Teleskops hervorgerufen. Im Bereich von 157° bis 203° liegt bei der 50 mm Blende (Basis 140 mm) immer eine Halterung in der Öffnung. Sobald sich die Öffnungen über die Halterungen bewegen, kommt es infolge des entstehenden Beugungsstreifens zu einem starken Kontrasteinbruch im Interferenzmuster. Im Grenzfall kann das Kontrastminimum nicht bestimmt werden. In diesem Fall ist die Bestimmung des Kontrastmaximums hilfreich, da sich bei dieser Methode der Kontrastverlust nicht so stark auswirkt.

10. Weitere Beobachtungen

Weitere Beobachtungsberichte über Gamma Virginis finden Sie in der Doppelstern Galerie und auf der Homepage von Wolfgang Vollmann. Er beobachtet Gamma Virginis bereits seit den 80er Jahren und verfolgte die Periastronpassage an einem 1m-Teleskop.

11. Quellennachweis

[1] Über die Bahnen der Doppelsterne gamma Virginis und zeta Herculis von Herrn Dr. Mädler, Astronomische Nachrichten, volume 16, p.33,
http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1839AN.....16...33M&amp;db_key=AST
[2] John Herschel, On the present apppearance of Gamma Virginis and sigma Lupi (Feb. 1836), Monthly Notices of the Royal Astronomical Society, Vol. 3, p.197, http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?1836MNRAS...3..197H
[3] Andreas Alzner, Objekte der Saison, gamma vir, Interstellarum 17, April 2001
[4] Wolfgang Vollmann, Gamma Virginis - die Periastronpassage 2005, interstellarum 33, April 2004, siehe auch http://members.eunet.at/vollmann/gamma_vir.htm
[5] Staffan Söderhjelm, Visual binary orbits and masses post Hipparcos, Astronomy and Astrophysics 341, S121-140, 1999
[6] Franz Kerschbaum, Ein visuelles Stern-Interferometer im Eigenbau, Sterne und Weltraum 4/1999, http://www.astro.univie.ac.at/~fzi/C11/interferometrie.html
[7] J. S. Schlimmer, Gamma Virginis - oder der Sieg über das Seeing, interstellarum 27, April 2003
[8] William I. Hartkopf, Brian D. Mason, & Gary L. Wycoff, U.S. Naval Observatory, Washington, DC, Fourth Catalog of Interferometric Measurements of Binary Stars http://ad.usno.navy.mil/wds/int4.html
[9] Brian Workman, Binary Star Orbit Calculator, http://www.geocities.com/CapeCanaveral/Runway/8879/englishdownload.html
[10] T.M. Girard Et Al, A Redetermination Of The Mass Of Procyon, Appendix : Astrometric Orbit Of Gamma Virginis, The Astronomical Journal 119, 2428-2436, May 2000
[11] http://ad.usno.navy.mil/wds/orb6/orb6frames.html
[12] IAU Commission 26, Circular Nr. 159, (Jun 2006)
[13] Mason, B.D, Hartkopf, W. I., Wycoff, G. L. Holdenried, E.R., Speckle Interferometry At The US NAVAL Observatory XII, Astronomical Journal, 132:2219-2230, November 2006
[14] Scardia et. al.,A Definitive Orbit for the Visual Binary ADS 8630 = γ Virginis, November 2006, http://www.mi.astro.it/docM/OAB/High/scardia_nov2006/index.html
[15] K.A.Strand, Reference : Ann. Sterrew. Leiden 18, 77; 1937
[16] W. Doberck, On the elements of the orbit of gamma Virginis, Astronomische Nachrichten, volume 141, p.57
[17]  Ephemeride von Henry Zirm, siehe Gamma Virginis im Periastron, interstellarum 51, April/Mai 2007

Danksagung
This research has made use of the Washington Double Star Catalog maintained at the U.S. Naval Observatory.


Letzte Aktualisierung : 05/2010, Seitenaufrufe seit 1. Januar 2005 :    © Copyright : www.epsilon-lyrae.de